Our research topics

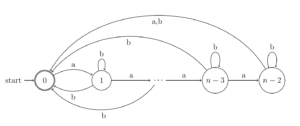
Basic research on automata and formal languages theory

Our group has developed basic research on regular languages and finite automata: automata minimality, indeterminism, reversibility and locality and  descriptive complexity, among other aspects. We have also approached the research of some aspects of linear languages: Equivalence, decidability and descriptive complexity. Similarly, we have focused on other kinds of formal languages based on structural information, such as tree languages and graph languages.

Machine learning

In the case of formal languages, our approach to machine learning is based in the perspective of Grammatical Inference which is a particular case of Inductive Inference as a learning technique. We have traditionally worked in Grammatical Inference on different  language classes, for example, regular, linear and context-sensitive languages. The inference of other kinds of structural languages, such as tree languages and graph languages, has also been addressed.

Criptography and cryptanalysis

Formal languages have been used classically in cryptography. For example, some methods of encryption based on abstract machines and permutation operations (as in the extended DES system) have been proposed. We have used basic concepts from the Formal Language Theory to propose new symmetric encryption methods and authentication systems that provide a new perspective to computational security.

Bioinformatics and systems biology

Biosecuences (textual representation of biomolecules, such as DNA, RNA and proteins) can be considered biochemically written languages that can be formalized through grammars and abstract machines. In this way, any set of biosecuences that could characterize some genomic aspect of interest (for example, mutations in DNA, structural features in RNA, or functional motifs in proteins) could be, a priori, studied under the paradigm of formal languages. Thus, from the automatic learning of these sequences, we have approached new genomic annotations and classifiers.

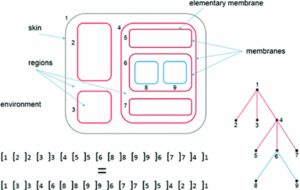Membrane computing and Natural Computing

In membrane computing, P systems are used as an abstraction of calculation machines inspired by the living eukaryotic cell. In the group we have worked on this paradigm and we have approached diverse aspects such as the importance of the structure of the systems in relation to the generative capacity of the same one, the relations between the P systems and the classic theory of the information, some relations between the P systems and some methods of machine learning. We have also proposed some variants of these systems and we have used them to solve highly complex problems.

In natural computing, we work with biocellular processing models (mainly, networks of bioinspired processors), biolanguages ​​and biomolecular computing models such as those inspired by DNA computing. We have proposed new variants of models and we have used them to solve real problems such as those in the bioinformatics and systems biology research fields.